【LC100】No240. 搜索二维矩阵 II

题目描述

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

• 每行的元素从左到右升序排列。

• 每列的元素从上到下升序排列。

提示:

• m == matrix.length

• n == matrix[i].length

• 1 <= n, m <= 300

• -109 <= matrix[i][j] <= 109

• 每行的所有元素从左到右升序排列

• 每列的所有元素从上到下升序排列

• -109 <= target <= 109

示例

示例 1：

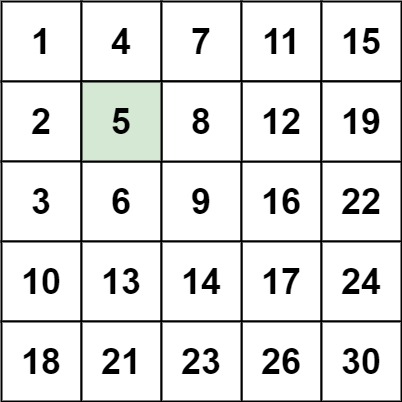
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

示例 2：

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

链接

思路

暴力gogogo！

解法一：暴力法

最先想到的肯定是暴力法，直接搜索查找。

代码

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return false;
        }
        int m = matrix.length;
        int n = matrix[0].length;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == target) {
                    return true;
                }
            }
        }
        return false;
    }
}

• 时间复杂度：O(n)

• 空间复杂度：O(1)

解法二：从右上角开始搜索

因为每行升序排列，每列也是升序排列，所以右上角是一个很神奇的数字。

当要查找的数字比右上角小时，代表右边这一列都搜索不到；比右上角大时，代表最上边这一行都搜搜索不到。

以这个逻辑逐步缩小搜索范围。

（同理左下角也行

代码

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return false;
        }
        int m = matrix.length;
        int n = matrix[0].length;
        int i = 0, j = n - 1;
        while (i < m && j >= 0) {
            if (matrix[i][j] == target) {
                return true;
            } else if (matrix[i][j] > target) {
                j--;
            } else {
                i++;
            }
        }
        return false;
    }
}

• 时间复杂度：O(n)

• 空间复杂度：O(1)